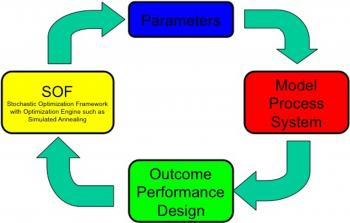
Many systems and processes, both natural and artificial, may be described by parameter-driven mathematical and physical models. These models are usually exercised in a forward-fashion: A certain set of values for the model-intrinsic parameters yields a corresponding outcome when processed through the model at hand. It is usually a straightforward task to define what an optimal outcome of the model is. Conversely, it is incomparably harder, if not impossible in many cases, to determine what the corresponding parameter values are that, when applied to the model, yield this outcome, or approximate it as closely as possible. If more than one set of parameter values yields the same desired outcome, the model is degenerate. One way to determine the optimal parameter values is to analytically invert the models, or to run them backwards. In many cases this is analytically or practically infeasible due to the complexity and high degree of non-linearity. To overcome this inherent problem, we have introduced a generally applicable Stochastic Optimization Framework (SOF) that can be interfaced to or wrapped around such models to effectively "invert" them. SOF allows for efficient sampling of the entire model-intrinsic parameter space by repeatedly running the respective model forward and by comparing the outcomes against the desired outcome, which results in a fitness measure. The goal of SOF is to optimize this fitness. Deterministic optimization techniques, such as gradient-based steepest-descent methods, are powerful and efficient in problems that exhibit only few local minima in the solution space. However, when dealing with multiple or infinite numbers of local minima, heuristic stochastic optimization methods, such as Simulated Annealing related algorithms, Genetic Algorithms, other Evolutionary Algorithms, and Genetic Programming, may become the prime methods of choice because of their capability to overcome local minima. The Visual and Autonomous Exploration Systems Research Laboratory at Caltech has long-term experience in the optimization of multi-dimensional systems and processes. Successful applications of SOF include protein design, robotics, device performance, space mission design, and parameter retrieval. Applications of SOF are manifold, such as in science, engineering, industry, defense & security, and reconnaissance/exploration.
Sponsor(s):